算是第一次完整的做的数模国赛A题,炉温曲线,经典的偏微分方程和优化问题(虽然此题也有常微分的解法)。从一开始的看国赛A题论文的看不懂,到了解它每一步建模的原理、每一步改变模型形式的用意,也算是完成了一个标准解决难啃骨头的流程。摆脱心理作用,一步步切实的学习,才能有所进步捏。
前言
算是鸽了很久的一次总结。恰好在抽出时间总结的这一天是人工智能专业的正式介绍日,也算是了解到了一波“未来可期”。大一是混沌的一年,带着高中的余念步入大学,显然是深受其害了,但还好没太走远。总觉得冥冥中有着些命运的指引,有些经历虽然“不堪回首“,但扎实起来自己,学学东西的感觉,还是挺不错的。
炉温曲线
一个炉子,一个\(0.15mm\)的金属件过炉,炉子分几个温度不同长度不同的大温区,每个大温区包含几个小温区,过炉过程中,金属件中心的温度变化曲线就是炉温曲线。
下面分别是炉子和炉温曲线的示意图:
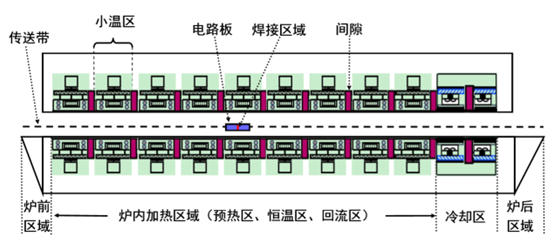
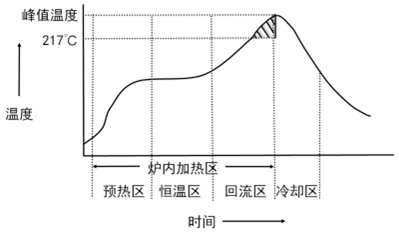
问题一
作为练习时长两月半的划水手,乍看此题,便觉得和18年国A的模型很相似。市面上虽然也有考虑热对流、热辐射的模型,但讲来讲去也只是来推导出一个牛顿冷却定律: \[ \frac {\partial T}{\partial x}=h[T_l(x)-T_x(x)] \] 那不妨我们就说这是道热传导的题。
对于热传导问题,我们对于其模型的创建,分为两步:
- 运用傅里叶定律(\(\large{\frac {\partial T}{\partial t}=\frac{k}{\rho c_p} \frac {\partial^2 T}{\partial^2 x}}\)),构建控制方程;
- 运用牛顿冷却定律,构建边界条件;
建立的热传导模型即为: \[ \begin{cases}{} \Large{\frac {\partial T}{\partial t}=\frac{k}{\rho c_p} \frac {\partial^2 T}{\partial^2 x}} \\ \large{k \frac {\partial T}{\partial x}=h[T_l(x)-T_x(x)]} \\ \end{cases} \] 为简化参数数量:我们设\(\alpha=\frac{k}{\rho c_p}\)。
这题有一说法是可以简化偏微分模型为微分模型,即不考虑在厚度只有\(0.15mm\)的金属件上的空间差分,转为\(T(t)\)的求解问题,运用: \[ \frac{T(n+1)-T(n)}{dt}=-k(T(t)-T_{air}(t)) \] 进行迭代求解。
第一问需要我们借助附件数据拟合出每个温区的热传导系数(由于每个温区的温度不同,器件的加热情况不同,所以其各类热力学参数也不同)。
温区间隔的温度变化
我们首先来处理小温区间隔之间的温度:
由于傅里叶定律告诉我们,\(\frac {\partial T}{\partial t}=\frac{k}{\rho c_p} \frac {\partial^2 T}{\partial^2 x}\),当温度稳定时,\(\frac {\partial T}{\partial t}=0\)(温度不随时间改变),所以$=0 $,空间偏导的二阶导为零,证明一阶导为常数,可推断出,间隔之间的温度变化为线性的,两个端点,分别就是两个小温区的温度。
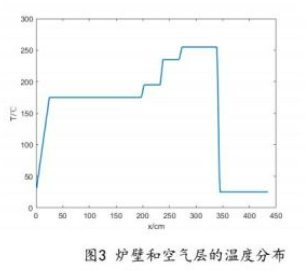
于是我们可以编得炉子温度分布函数:
%炉内温度分布
function Tu=TEMP(x)
Kelvin=273.15;%换成华氏
global T1 T2 T3 T4
if x<25
Tu=(T1-25)/(25-0)*(x-0)+25+Kelvin;
elseif x<197.5
Tu=T1+Kelvin;
elseif x<202.5
Tu=(T2-T1)/5*(x-197.5)+T1+Kelvin;
elseif x<233
Tu=T2+Kelvin;
elseif x<238
Tu=(T3-T2)/5*(x-233)+T2+Kelvin;
elseif x<268.5
Tu=T3+Kelvin;
elseif x<273.5
Tu=(T4-T3)/5*(x-268.5)+T3+Kelvin;
elseif x<339.5
Tu=T4+Kelvin;
elseif x<344.5
Tu=(25-T4)/5*(x-339.5)+T4+Kelvin;
else
Tu=25+Kelvin;
end
endCrank-Nicalson格式的有限差分法
由于这题金属件的厚度只有\(0.15mm\),运用显式差分时极易不收敛,所以我们采用\(Crank-Nicalson\)格式的差分法(其具体推导可见差分法那一篇文章): \[ \begin{bmatrix} \frac{k}{dx}+h & -\frac{k}{dx} & \cdots & \cdots \\ \beta & -(1+2\beta) & -\beta & \cdots \\ & \ddots & \ddots & \ddots \\ \cdots & \beta & -(1+2\beta) & -\beta \\ \cdots & \cdots & -\frac{k}{dx} & \frac{k}{dx}+h \end{bmatrix} \begin{bmatrix} T^{n+1}_1\\ T^{n+1}_2 \\ \vdots\\ T^{n+1}_{m-1}\\T^{n+1}_{m} \end{bmatrix} =S \]
\[ S= \begin{bmatrix} -1+2\beta & -\beta & \cdots & \cdots \\ -\beta & -1+2\beta & -\beta & \cdots \\ & \ddots & \ddots & \ddots \\ \cdots & -\beta & -1+2\beta & -\beta \\ \cdots & \cdots & -\beta & -(1+2\beta) \end{bmatrix} \begin{bmatrix} T^{n}_1\\ T^{n}_2 \\ \vdots\\ T^{n}_{m-1}\\T^{n}_{m} \end{bmatrix} \]
再将\(S(1)、S(i_{max})\)修正为\(hT_{env}\)
该差分法的程序如下:
% 构造M系数矩阵的框架及其第一行和最后一行
A=alpha1*dt/(2*dy*dy);
M=eye(length_y,length_y);
M(1,1)=h+k/dy;
M(1,2)=-k/dy;
M(length_y,length_y-1)=-k/dy;
M(length_y,length_y)=h+k/dy;
% 完整构建M系数矩阵
for index_x=2:length_y-1
M(index_x,index_x-1)=A;
M(index_x,index_x)=-2*A-1;
M(index_x,index_x+1)=A;
end
% 隐式求解
N=zeros(length_y,1);
for index_t=2:348
x=(index_t-1)*dt*v;
Tu=TEMP(x);
N(1)=h*Tu;
N(length_y)=h*Tu;
% 求出S的值,此处是N矩阵
for index_x=2:length_y-1
N(index_x)=-A*(T(index_x+1,index_t-1)+T(index_x-1,index_t-1))+(2*A-1)*T(index_x,index_t-1);
end
% 利用右除,算出T=M的逆*N,完成迭代
T(:,index_t)=M\N;
end随后需要进行最优参数拟合,考虑到不同温区的传热系数不同,我们需要进行遍历寻找的最优参数解空间即为: \[ \large{[k、h、\alpha_1、\alpha_2、\alpha_3、\alpha_4、\alpha_5]} \] 借助附件数据,我们得知温度的差分最大不超过个位数限制,因此可知\(\Large{\frac{\alpha dt}{dx^2} }\)为个位数数量级。附件中取\(dt=0.5\),我们照取。由于金属件厚度为\(0.15mm\),我们取\(dx=10^{-6}m\),可得\(\alpha\)的数量级为\(10^{-11}\)。由于解空间较大,我们先在\(10^{-11}\)数量级中寻找\(\alpha\),查阅相关资料后,确定在10~30中搜索\(h\),在\(10^{-6}\)数量级中搜索\(k\)。
则,完整的拟合最优参数代码为:(简略搜索版)
clear all
clc
global T1 T2 T3 T4
T1=175;
T2=195;
T3=235;
T4=255;
Kelvin=273.15;
load standard.mat
t_max=standard(end,1);
dy=1e-6;
dt=0.5;%题目要求
y_max=0.15e-3;
v=70/60;%单位cm/s
length_y=round(y_max/dy+1);
length_t=round(t_max/dt+1);
standard(:,2)=standard(:,2)+Kelvin;%换温标
Errormin=inf;
Error_pre=[];
%确定搜索步长
dk = 1e-6;
dh = 1;
da = 1e-11;
for k=1e-6 : dk : 1e-5
for h=10 : dh :30
for alpha1=1e-11 : da :1e-10
for alpha2=1e-11 : da :1e-10
for alpha3=1e-11 : da :1e-10
for alpha4=1e-11 : da :1e-10
for alpha5=1e-11 : da :1e-10
T=zeros(length_y,length_t);
T(:,1)=ones(length_y,1)*(25+Kelvin);
%区域1
A=alpha1*dt/(2*dy*dy);
M=eye(length_y,length_y);
M(1,1)=h+k/dy;
M(1,2)=-k/dy;
M(length_y,length_y-1)=-k/dy;
M(length_y,length_y)=h+k/dy;
for index_x=2:length_y-1
M(index_x,index_x-1)=A;
M(index_x,index_x)=-2*A-1;
M(index_x,index_x+1)=A;
end
N=zeros(length_y,1);
for index_t=2:348
x=(index_t-1)*dt*v;
Tu=TEMP(x);
N(1)=h*Tu;
N(length_y)=h*Tu;
for index_x=2:length_y-1
N(index_x)=-A*(T(index_x+1,index_t-1)+T(index_x-1,index_t-1))+(2*A-1)*T(index_x,index_t-1);
end
T(:,index_t)=M\N;
end
%区域2
A=alpha2*dt/(2*dy*dy);
for index_x=2:length_y-1
M(index_x,index_x-1)=A;
M(index_x,index_x)=-2*A-1;
M(index_x,index_x+1)=A;
end
N=zeros(length_y,1);
for index_t=349:409
x=(index_t-1)*dt*v;
Tu=TEMP(x);
N(1)=h*Tu;
N(length_y)=h*Tu;
for index_x=2:length_y-1
N(index_x)=-A*(T(index_x+1,index_t-1)+T(index_x-1,index_t-1))+(2*A-1)*T(index_x,index_t-1);
end
T(:,index_t)=M\N;
end
%区域3
A=alpha3*dt/(2*dy*dy);
for index_x=2:length_y-1
M(index_x,index_x-1)=A;
M(index_x,index_x)=-2*A-1;
M(index_x,index_x+1)=A;
end
N=zeros(length_y,1);
for index_t=410:470
x=(index_t-1)*dt*v;
Tu=TEMP(x);
N(1)=h*Tu;
N(length_y)=h*Tu;
for index_x=2:length_y-1
N(index_x)=-A*(T(index_x+1,index_t-1)+T(index_x-1,index_t-1))+(2*A-1)*T(index_x,index_t-1);
end
T(:,index_t)=M\N;
end
%区域4
A=alpha4*dt/(2*dy*dy);
for index_x=2:length_y-1
M(index_x,index_x-1)=A;
M(index_x,index_x)=-2*A-1;
M(index_x,index_x+1)=A;
end
N=zeros(length_y,1);
for index_t=471:592
x=(index_t-1)*dt*v;
Tu=TEMP(x);
N(1)=h*Tu;
N(length_y)=h*Tu;
for index_x=2:length_y-1
N(index_x)=-A*(T(index_x+1,index_t-1)+T(index_x-1,index_t-1))+(2*A-1)*T(index_x,index_t-1);
end
T(:,index_t)=M\N;
end
%区域5
A=alpha5*dt/(2*dy*dy);
for index_x=2:length_y-1
M(index_x,index_x-1)=A;
M(index_x,index_x)=-2*A-1;
M(index_x,index_x+1)=A;
end
N=zeros(length_y,1);
for index_t=593:747
x=(index_t-1)*dt*v;
Tu=TEMP(x);
N(1)=h*Tu;
N(length_y)=h*Tu;
for index_x=2:length_y-1
N(index_x)=-A*(T(index_x+1,index_t-1)+T(index_x-1,index_t-1))+(2*A-1)*T(index_x,index_t-1);
end
T(:,index_t)=M\N;
end
%最小二乘
dT=T(76,39:end)-standard(:,2)';
Error=sum(dT.*dT)/length(standard);
Error_pre=[Error_pre Error];
if Error<Errormin
Errormin=Error;
alpha=[alpha1,alpha2,alpha3,alpha4,alpha5];
kmin=k;
hmin=h;
end
end
end
end
end
end
end
end
%plot(1:length_t,T(76,:),'b');
%hold on
%plot(39:747,standard(:,2))搜索到解空间大致范围后,再进行数量级更小的精细搜索。得到最优参数,便能算出新温度组下的炉温曲线。
(虽然这简单一句话,包含着好几小时的matlab遍历用时)
问题二
问题二要求我们在满足制程界限的前提下,寻找最大的过炉速度。这是一道很明显的有约束条件的优化问题。则我们把整个速度区间遍历,满足制程界限的留下,不满足的删除,然后去确定留下的速度中最大的速度即可,并且也是采用先粗略遍历,再在最优解附近以更高精度遍历的方法。
(制程界限是针对于炉温曲线来要求的)
制程界限带来的约束条件为:
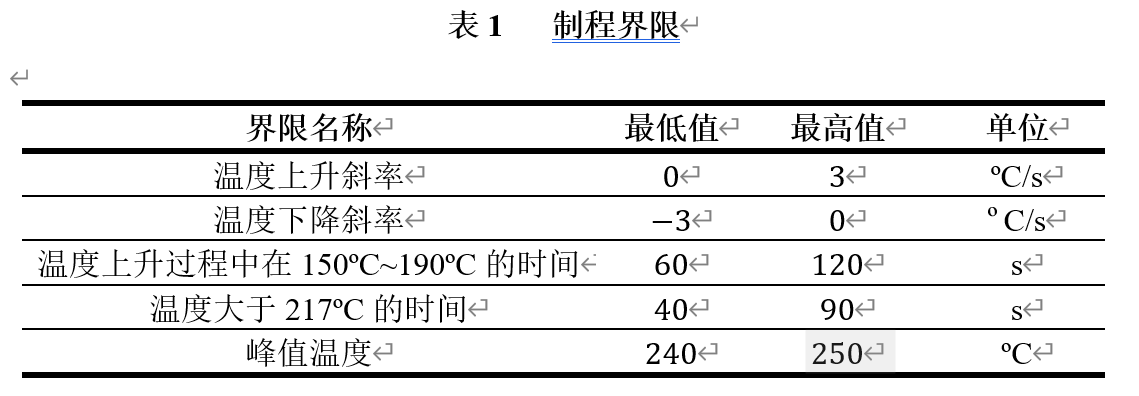
转化为数学语言即为: \[ s.t. \large{ \begin{cases} 240\leqslant \text{max}[T(t)]\leqslant250\\ \text{max}[|T'(x)|] \leqslant3\\ 60\leqslant t|_{[150\leqslant T(t)\leqslant190,T'(t)>0]}\leqslant120\\ 40 \leqslant t|_{[T(t)\geqslant217]}\leqslant90 \end{cases} } \] 我们设置一个\(flag\)函数,当\(v\)满足约束条件时,\(flag=1\),当不满足约束条件时,\(flag=0\),以此来保留和去除\(v\)。代码如下:(其中的BoxValue是用于第四问的对称指标来用的)
function flag=restrict(T,dt)
global BoxValue
T=T-273.15;%改成摄氏度便于写条件
dT=T(2:end)-T(1:end-1);
k=[0 dT/dt];%为了下面计数的方便
HeatUpLimit=0;
ExtrameHeatLimit=0;
Box=[];
for i=1:length(T)
if k(i)>0 && T(i)>150 && T(i)<190
HeatUpLimit=HeatUpLimit+1;
elseif T(i)>217
Box=[Box i];
ExtrameHeatLimit=ExtrameHeatLimit+1;
end
end
HeatUpTime=HeatUpLimit*dt;
ExtrameHeatTime=ExtrameHeatLimit*dt;
[HighestLimit,PeakIndex]=max(T);
PeakIndex
Box(1)
Box(end)
BoxValue=(2*PeakIndex-Box(1)-Box(end))*dt;
if max(k)>3 || min(k)<-3
flag=0;
elseif HighestLimit>250 || HighestLimit<240
flag=0;
elseif HeatUpTime<60 || HeatUpTime>120
flag=0;
elseif ExtrameHeatTime<40 || ExtrameHeatTime>90
flag=0;
else
flag=1;
end
end
再在利用该函数保留下来的速度中,寻找最大的一个即可。(同时注意速度的单位转换)