作为数模培训的第一课,差分方程确实帮助我对数模建立起了比较浓厚的兴趣,作为一种递推关系式,它的暴力求解和迭代后的神奇性质,在解决很多实际问题以及进行数值分析时,都起到了很关键的作用。
差分方程的定义
(即使由于写文章的需要再去听了一遍课,我也没能清楚它的定义到底是啥)
无奈在这里借用一下百度百科的介绍:
在数学上,递推关系(recurrence relation),也就是差分方程(difference equation),是一种递推地定义一个序列的方程式:序列的每一项目是定义为前一项的函数。某些简单定义的递推关系式可能会表现出非常复杂的(混沌的)性质,他们属于数学中的非线性分析领域。
嗯~,递推关系就是差分方程。谈到递推关系,也就不得不想到神奇的斐波那契了,那堂数模课也是由此展开的。
斐波那契
它的神奇不必多说,这里直接给出它的递推关系: \[ a_0=0,a_1=1 ,a_n=a_{n-1}+a_{n-2} \quad(n>=2,n \in \natnums) \] 差分方程上来就惊我一下,给出了它的通项公式: \[ a_n=\frac{1}{\sqrt []{5}}[(\frac{(1+\sqrt []{5})}{2})^n-(\frac{(1-\sqrt []{5})}{2})^n] \] 以下是它的求解过程:
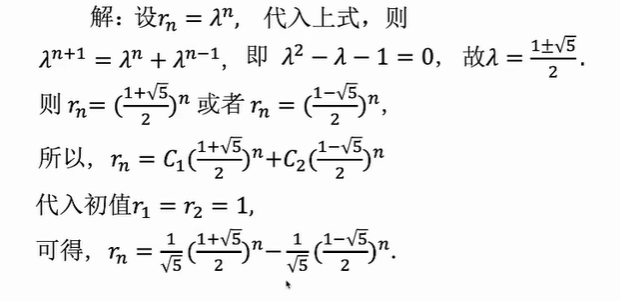
其中\(r_n\)就是\(a_n\),嗯~,暴力假设,可能不专业的说,\(\lambda^n\)是差分方程的特征算子,\(\lambda\)是特征根,由此得出通解,带入原始数据,得到解,即这个递推公式的通项公式。
人总有一种本能,只有知道它每一步到底是什么,才会让人踏实。斐波那契显然给足了我安全感,解出它的通项,它在数学上的神秘就具体多了。但这种点亮战争迷雾般的手段,确实是通法,但有时却极难操作(三角形重心序列问题),\(\lambda\)有时会出现复数解、含n解,会让最后解的确立十分麻烦,成为一个比拼眼力的过程。但好在,差分方程能被研究的如此之多,它的作用显然不只是给出安全感这么简单。
差分方程的平衡解及其稳定性
直接看图:

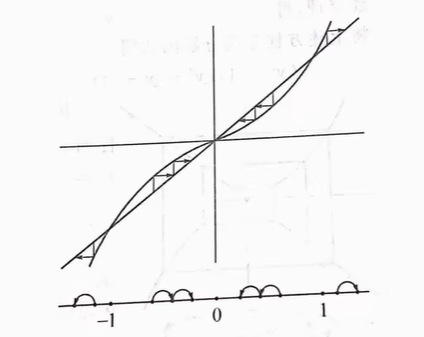
其中\(x=0\)具有吸引性,\(x=-1\quad x=1\)具有排斥性,稳定集为\((-1,1)\)。
为什么说0,1,-1是系统的平衡点,因为当\(x\)的初始值取在这三个点时,无论进行多少次递推,\(x_n\)都保持这个初始值不变,所以它是平衡的。当初始值落在\((-1,1)\)时,进过多次递推迭代,\(x_n\)的值会最终趋向0,而在之外的初始值,迭代过后的最终会无穷大,这就是吸引与排斥。
这便体现出差分方程的其它重要作用——预测迭代趋势和求出平衡解等式的根。这在实际应用和数值分析中十分重要。
但它的神奇远不止于此,它的独特混沌性,在密码学中大有作用。有人也说,差分方程是离散的微分方程,微分方程是连续的差分方程,它和微分方程之间的关系,也值得我去理解一番,但作为对差分方程的一个初步了解,这篇文章想必已能达到这个目的。