差分方程数模课的一道练习题——差分方程暴力求通项的极致?原本这种苦人力的方式只是起训练作用,但含复数解的三角函数转换和欧拉公式的运用,使这题有浅记录一下的必要。
求解特征根
题目如下
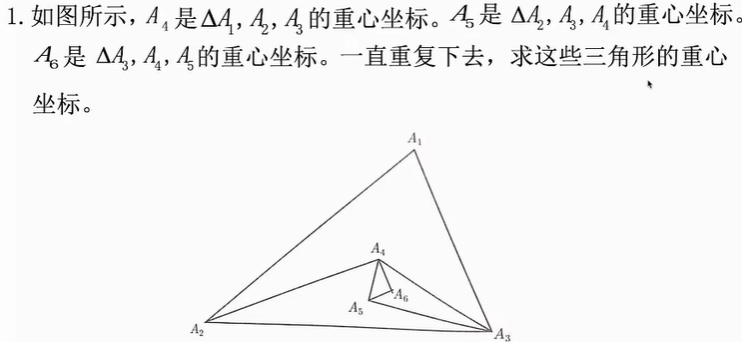
它的递推关系很好建立:(通过三角形的重心性质) \[ x_{n+3}=\frac{x_n+x_{n+1}+x_{n+2}}{3},\qquad y_{n+3}=\frac{y_n+y_{n+1}+y_{n+2}}{3} \] 运用差分方程1中所学到的假设方法,设\(x_n=\lambda^n\),则原等式两边同时消去\(\lambda^n\)得: \[ 3\lambda^3=\lambda^2+\lambda+1 \] 易看出\(\lambda_1=1\)是该特征方程的一个解,按照解三次方程的方法,移项,提出一个\((\lambda-1)\)得: \[ (\lambda-1)(3\lambda^2+2\lambda+1)=0 \] 通过后面括号的式子,得出\(\lambda\)的另两个复数解: \[ \lambda_2=\frac{-1+i\sqrt[]{2}}{3},\lambda_3=\frac{-1-i\sqrt[]{2}}{3} \] 于是可以得出:
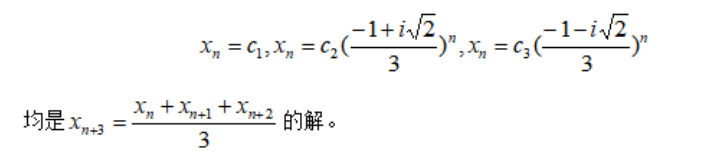
复数解化三角函数
这时我们来分析一下,三角形的重心坐标一直在实数坐标系上迭代,其特解一定为实数(不是复数),因而我们需要得出两个复数解的n次方后得到的实数是什么,即如何消去虚数部分。n次方的结果我们难以计算,且考虑到三角函数具有特殊的0,1性质,我决定将复数解转化为三角函数形式进行后续处理。 \[ (\frac{-1+i\sqrt[]{2}}{3})^n=(\frac{1}{\sqrt[]{3}})^n(cos\theta+isin\theta)^n=(\frac{1}{\sqrt[]{3}})^n(cos(n\theta)+isin(n\theta)) \] 其中: \[ cos\theta=-\frac{1}{\sqrt[]{3}},sin\theta=\frac{\sqrt[]{2}}{\sqrt[]{3}} \] 前一个等式变化属于高中常用的三角变换,也就是复数解化三角函数的技巧所在。
棣莫弗定理
后面一个等式变化则用到了欧拉公式,先介绍一下欧拉公式的内容:
\(e^{ix}=cosx+isinx\)
\((e^{ix})^n=e^{inx}\)
\(e^{i(nx)}=cos(nx)+isin(nx)\)
欧拉公式的证明并不难,把等式两边都泰勒展开即可证出相等。
对本题,先将三角函数收成\(e^{ix}\),再n次方之后再展开,就完成了等式变换,这个等式就被称为棣莫弗定理。
留给访问者
但很可惜,即使化成最后的三角函数形式,我也无法看出最后的实数解到底是什么样子的。
解答中是这样说的:

这个《通过仔细的计算》之后得到实数解着实太过玄学,得出通解后,带入初始数据\(x_1,x_2,x_3\)(对应\(n=1,2,3\))即可解得特解,而后得出重心的每个坐标。而这个实数解的得出就留给访问者来解决吧,学会了欧拉公式和复数解,我已可以鸣金收兵了。