用较简单的函数来近似复杂函数的问题,就是函数逼近问题,曲线拟合和函数插值是数值分析中常用的两种函数逼近方法。在整体上要求拟合的比较好,就是曲线拟合问题;要求简单函数的曲线通过所有的给定点,就是函数插值问题,可以通过matlab快速地利用离散点来获得函数曲线。线性问题一般易于讨论和研究。因此,线性拟合坐属曲线拟合的一种,研究加入了回归分析,用以体现拟合曲线的数理统计意义,称为线性回归。
曲线拟合与最小二乘法
一元回归方程(经验回归方程)
一元线性回归方程的模型为: \[ Y=\beta_0+\beta_1X+e,\quad E(e)=0\\Y=f(x)+e \]
\(f(x)\)为\(X\)能决定的部分,\(e\)为其他未考虑的因素,每次带入的\(x_i\)不同,对应的\(e_i\)也不同,但总体\(e\)需要满足零均值、等方差、不相关的要求。
其中\(\beta_0和\beta_1\)的值可以用简单的统计方法求出。
解上述方程可以求得a和b。通常将a和b的计算公式写为如下形式:
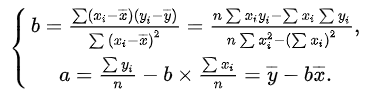
多元回归方程
多元回归方程的模型为: \[ Y=\beta_0+\beta_1X_1+...+\beta_{p-1}X_{p-1}+e \]
假设对\(Y、X、...X^{P-1}\)得到了n组观测值: \[ y_i、X_{i1}、X_{i2}、...X_{in} \] 注意,这里除去\(y_i\),共有\(p*n\)组数据(默认\(\beta_0\)是\(X_0\)的系数,且\(X_0\)每次取值均为1)。
则,多元回归模型的矩阵形式为: \[ y=X\beta+e \]
其中: \[ y=\begin{bmatrix} y_1 \\ y_2 \\ \vdots \\y_n \end{bmatrix}, X=\begin{bmatrix}1 & x_{11} & \cdots & x_{1p-1} \\ 1 & x_{21} & \cdots & x_{2p-1}\\ \vdots & \vdots & \vdots & \vdots \\ 1 & x_{n1} & x_{n2} & x_{np-1}\end{bmatrix}, \beta=\begin{bmatrix} \beta_1 \\ \beta_2 \\ \vdots \\\beta_{p-1} \end{bmatrix}, e=\begin{bmatrix} e_1 \\ e_2 \\ \vdots \\e_n \end{bmatrix} \]
(其中,\(y\)称为观测向量,\(X\)称为已知矩阵,\(\beta\)称为未知参数向量,\(e\)称为随机误差向量)
最小二乘法
任务是要解出\(\beta\)这个未知参数向量。寻找最优的\(\beta\),它能使\(e\)的长度最小,简单来说,由于追求求导后运算的方便,一般是使\(e\)的长度的平方最小,即: \[ minQ(\beta)=\Vert {e} \Vert^2=\Vert {y-X\beta} \Vert^2=(y-X\beta)^T(y-X\beta) \]
我们想要求出\(\beta\)的估计\(\hat{\beta}\),就得求出使这个式子最小值点,这就需要用到矩阵求导的知识对这个式子进行求导。
矩阵求导
矩阵,也可以说成是向量,对于一个\(Y=f(x)\)来说,\(Y\)和\(x\)既可以是标量,也可以是向量(也就是矩阵)。因此,我们既可以对一个标量求它的向量自变量的导数,也可以对一个向量求它的标量或向量自变量的导数。这和标量对标量求导是一样的,只不过是有不同的规则。在矩阵的运用上,这点已经十分成熟,向量的灵活使用,大大减小了计算机的运算量。
矩阵求导有着这样的口诀:
- 标量不变,向量拉伸
- \(Y\)横向拉,\(x\)纵向拉
例如:(部分负号使用不严谨,不过不影响理解)


都是向量则分个先后分别拉伸就行。
依据这个原理我们可以得到两条矩阵求导的常用结论:(这里\(A=a^T\))
当\(f(x)=\sum_{i=1}^na_ix_i=A^Tx=x^TA\)时,\(\frac{df(x)}{dx}=\frac{dA^Tx}{dx}=\frac{dx^TA}{dx}=A\)
当\(f(x)=\sum_{i=1}^n\sum_{j=1}^na_ix_ix_j=x^TAx\)时,\(\frac{df(x)}{dx}=\frac{dx^TAx}{dx}=(A+A^T)x\)
回到最小二乘法
让我们把这个式子的右边继续写下去: \[ minQ(\beta)=\Vert {e} \Vert^2=\Vert {y-X\beta} \Vert^2=(y-X\beta)^T(y-X\beta)\\ =y^Ty- \beta^T X^T y-y^TX\beta + \beta^TX^TX\beta\\ =y^Ty- 2y^TX\beta + \beta^TX^TX\beta \] 将这个式子左右两边对\(\beta\)求导: \[ minQ(\beta)'=0-2(y^TX)^T+(X^TX+(X^TX)^T)\beta\\ =-2X^Ty+2X^TX\beta \] 令这个式子等于0,可得: \[ \hat{\beta}=(X^TX)^{-1}X^Ty \] 由此便可以通过已知的\(X、y\)求出\(\hat{\beta}\)。得到拟合的多元回归方程。
函数插值
也是一种函数逼近的方法,给人直观的感受就是用平滑的曲线连接一堆离散的点。得到的这一曲线可以用于计算某些离散点之间未给出点的值,起到最大限度根据离散点还原原连续函数的效果。
借助强大的matlab,我们通过spline(x值,y值,插值区间)函数,就可以很便捷的完成三次样条插值。
同时,可以用pp=spline(x,y)来获取三次样条插值函数,并接着可以使用y=ppval(pp,自变量),来求出插值函数上某点的y值,非常好用~~。